2022年の年初の予想をされているブロガーさん達も多いように感じます。
予想が当たるかどうかはわかりませんが、観察をする準備をしておいたり、過去どうだったのかを確認しておくのは大事だと思います。データをもとに現状を確認し、その先行きを考えてみたいと思います。
現状認識・本記事の目的
FRB(米連邦準備制度理事会)による利上げ、金利上昇が目前に迫る状態の中、居心地のよい株式市場、カネ余り状態からの大きな変化をマーケットは織り込んでいるのでしょうか。日用品の価格の上昇や、不動産価格に代表されるリスクアセットなど、インフレという言葉も日常的に目にするようになってきています。
金利の動向とグロース株との連動性・相関の高さを指摘するコメントもあるようです。

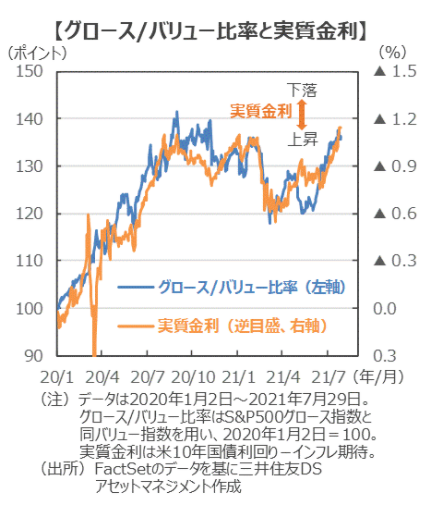
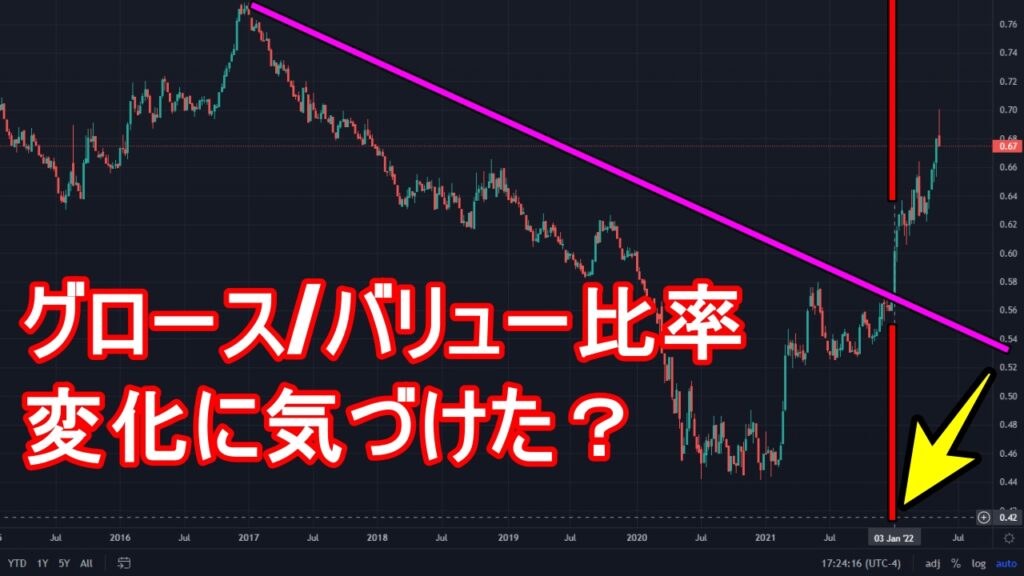
今後の展開を実質金利とグロース/バリュー比率の視点から見ていきたいと思います。
データの取得
今回は以前書いた記事 【コピペで動く!】「新規保険失業申請件数の反転」は未来を占うのか?! (Python コードあり) Twitterで出てくる知見は本当か自分で調べてみよう。2【違いをみつけろ!】を参考にセントルイス連銀のサイトとYahoo-US!のサイトのデータを結合しながら解析してみたいと思います。
セントルイス連銀のサイトからのデータ取得はこちらの記事も参考になります。
【コピペで動く!】ゴールドと米国の実質金利の今後の動向について。WebサービスとPythonと両方で確認!
Yahoo-US!からのデータ取得はこちらの記事を参考にしてください。
米国株式に変調の兆し?資金に安全な避難場所はあるのか? 【コピペで動く!】米国株式と債券、ゴールドの相関をPythonで確認
Pythonによる分析
セントルイス連銀 からのデータ取得
まずは セントルイス連銀のサイトFREDからをデータ取得します。
import pandas_datareader.data as web
import datetime
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# 可視化のためのセットです。
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
#import statsmodels.api as sm
import matplotlib.dates as mdates
import warnings
warnings.filterwarnings('ignore')
start_D = datetime.datetime(2020, 1, 1)
end_D = datetime.datetime.today()
df1 = web.DataReader([
"SP500",
"DFII10", #Market Yield on U.S. Treasury Securities at 10-Year Constant Maturity, Inflation-Indexed
], "fred", start_D, end_D)
#print(stock.describe)
#print(type(stock.index))
#print(stock.head())
display(df1.head(2).append(df1.tail(3)))
display(type(df1))
plt.plot(df1.index,df1["DFII10"])
plt.show()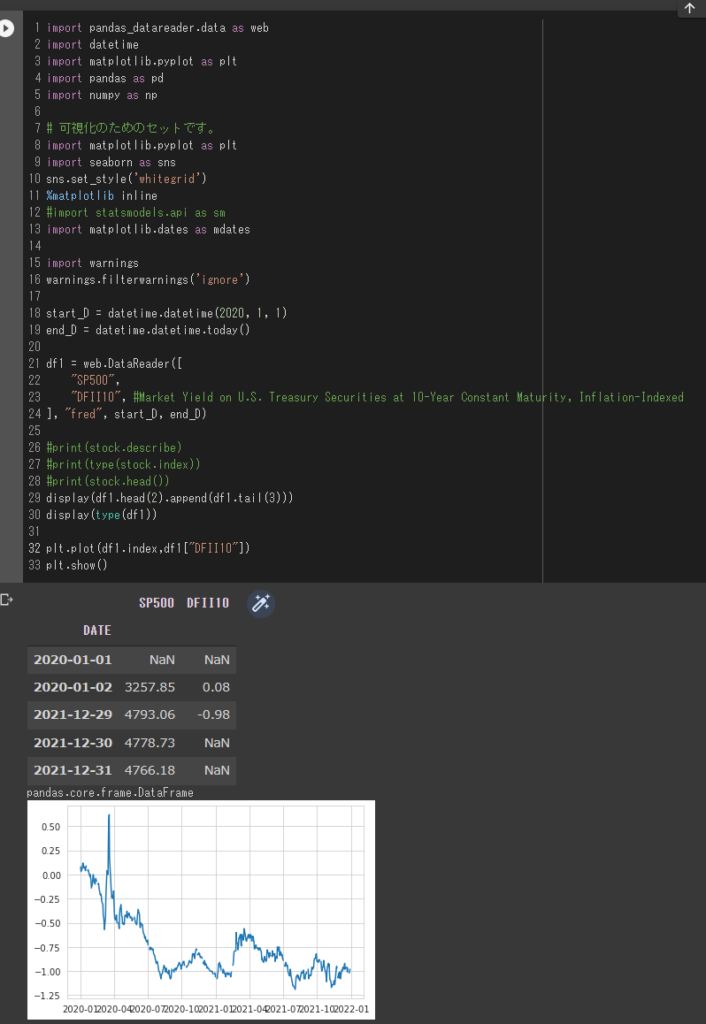
上記レポートでは実質金利のY軸は逆軸になってますので、まずはそこを確認します。

plt.ylim(df1["DFII10"].max(),df1["DFII10"].min())
plt.plot(df1.index,df1["DFII10"])
plt.show()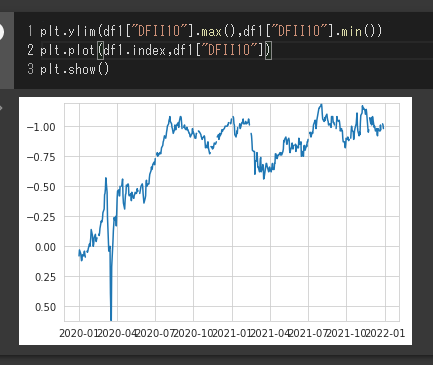
データ自体は問題ないようです。
Yahoo-US!からのデータ取得
今回はグロース/バリュー比率を求める必要がありますので、iSharesのスタイル型のETF
IVW:iShares S&P500 Growth ETF
IVE:iShares S&P500 Value ETF
を読み込むことにします。

コード自体はこちらになります。
!pip install yfinance --upgrade --no-cache-dir
import yfinance as yf
codelist1 = [
"^GSPC",
"IVW","IVE"
]
df3 = yf.download(codelist1, start=start_D, end=end_D)["Adj Close"]
display(df3.head(2).append(df3.tail(2)))
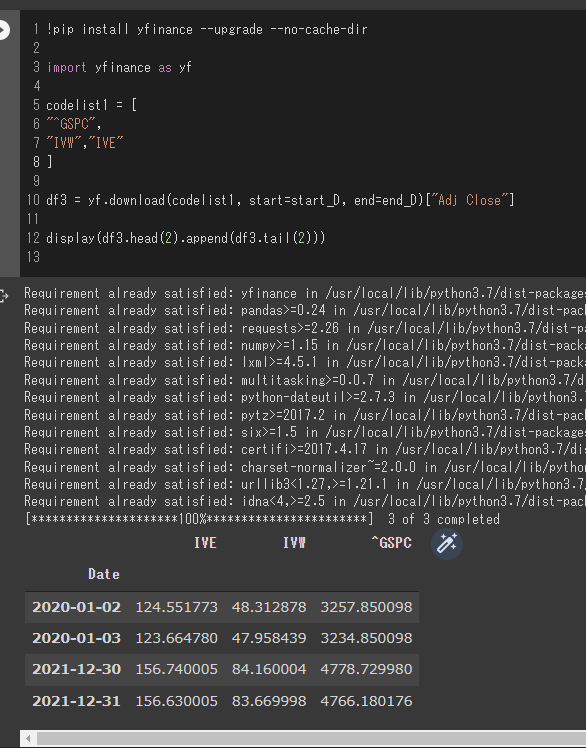
グロース/バリュー比率とのことなので、グロース(IVW)をバリュー(IVE)で割ったものを定義します。
df4=df3.copy()
df4["GV"]=df4["IVW"]/df4["IVE"]
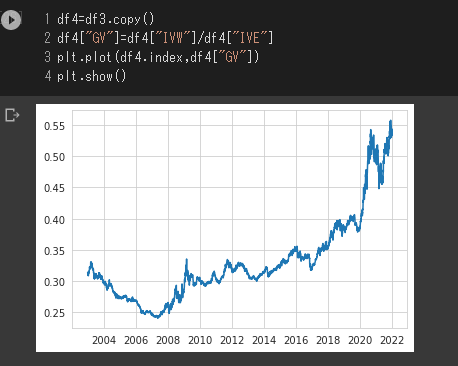
plt.plot(df4.index,df4["GV"])
plt.show()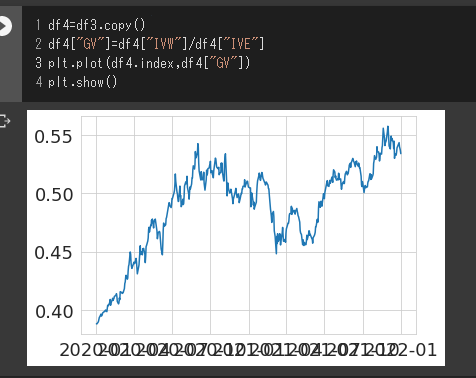
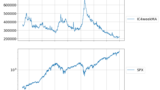
二つのグラフの重ね合わせ
実質金利とグロース/バリュー比率のデータが取得できましたので、二つのグラフを重ね合わせてみます。
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.plot(df1.index,df1["DFII10"],color="blue")
ax1.invert_yaxis()
ax2.plot(df4.index,df4["GV"],color="red")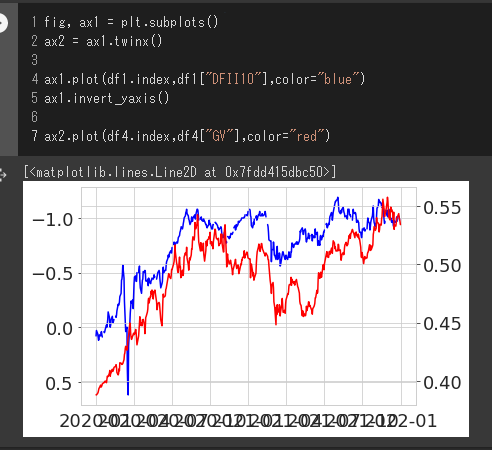
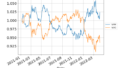
上記レポートでは2020年1月2日を100とした指数で出していますが、同じ傾向が見て取れるのが分かると思います。

今後は実質金利にグロース/バリュー比率が影響を受けるようにも思えますが、2020年以前はどうだったのでしょうか?直近2年間だけ相関が高かったり、金利の数値の絶対値などでは影響を受けないのでしょうか?
セントルイス連銀のサイトFREDから実質金利のデータが取れる2003年からのデータで改めて確認してみたいと思います。
今回は start_D = datetime.datetime(2003, 1, 1) として上記コードを再度走らせ直してみたいと思います。
import pandas_datareader.data as web
import datetime
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# 可視化のためのセットです。
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
#import statsmodels.api as sm
import matplotlib.dates as mdates
import warnings
warnings.filterwarnings('ignore')
start_D = datetime.datetime(2003, 1, 1)
end_D = datetime.datetime.today()
df1 = web.DataReader([
"SP500",
"DFII10", #Market Yield on U.S. Treasury Securities at 10-Year Constant Maturity, Inflation-Indexed
], "fred", start_D, end_D)
#print(stock.describe)
#print(type(stock.index))
#print(stock.head())
display(df1.head(2).append(df1.tail(3)))
display(type(df1))
plt.plot(df1.index,df1["DFII10"])
plt.show()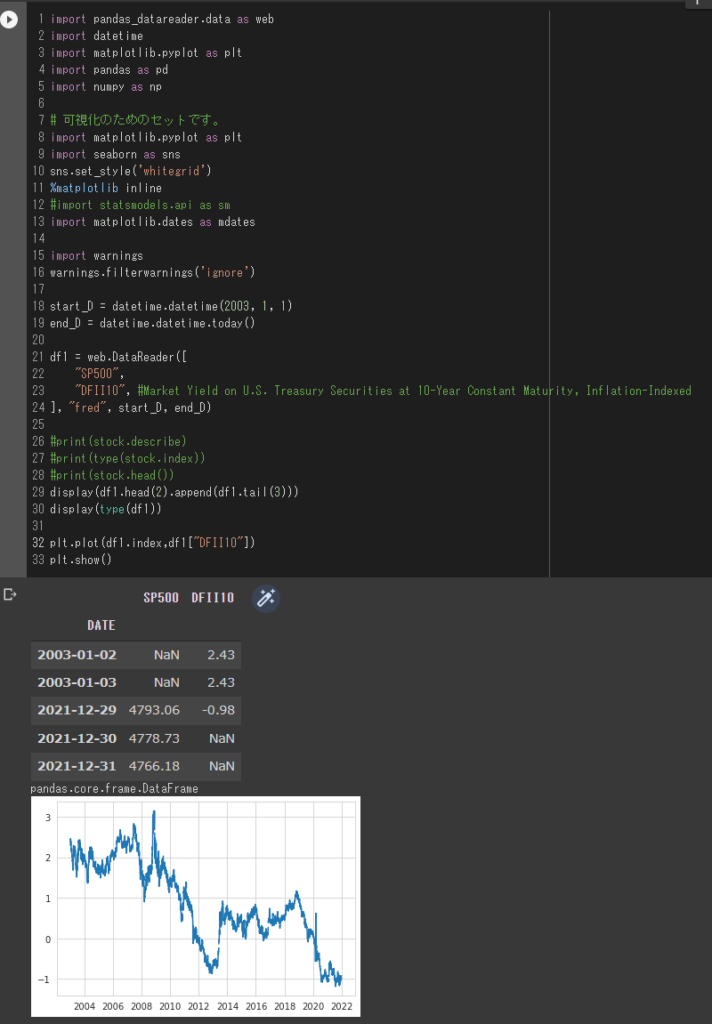
!pip install yfinance --upgrade --no-cache-dir
import yfinance as yf
codelist1 = [
"^GSPC",
"IVW","IVE"
]
df3 = yf.download(codelist1, start=start_D, end=end_D)["Adj Close"]
display(df3.head(2).append(df3.tail(2)))
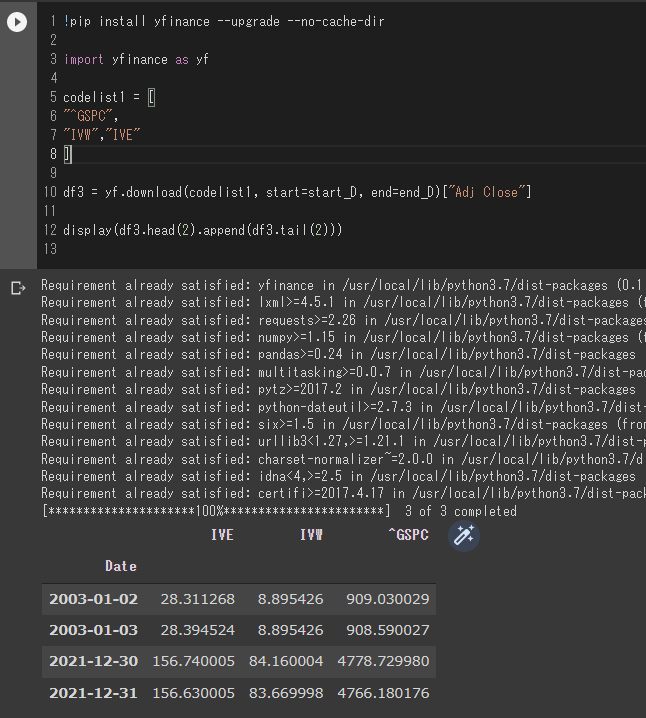
df4=df3.copy()
df4["GV"]=df4["IVW"]/df4["IVE"]
plt.plot(df4.index,df4["GV"])
plt.show()
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.plot(df1.index,df1["DFII10"],color="blue")
ax1.invert_yaxis()
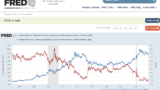
ax2.plot(df4.index,df4["GV"],color="red")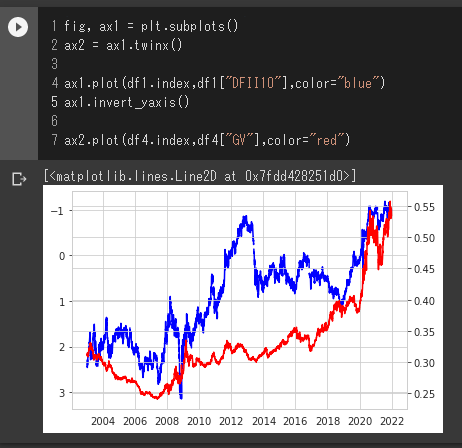
となるようです。今回は金利上昇ということですので、2013年に注目した場合 グロース/バリュー比率 は確かに下がっているようですが、その期間のS&P500は大きなドローダウンもなく上昇しているようにも見えます。
Zone1_start = datetime.datetime(2012,10,1)
Zone1_end = datetime.datetime(2013,11,1)
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.plot(df1.index,df1["DFII10"],color="blue")
ax1.invert_yaxis()
ax2.plot(df4.index,df4["GV"],color="red")
ax1.axvspan(Zone1_start,Zone1_end, color = "gray", alpha=0.3)
plt.show()
fig, ax3 = plt.subplots()
ax4 = ax3.twinx()
ax3.plot(df1.index,df1["DFII10"],color="blue")
ax3.invert_yaxis()
ax4.plot(df4.index,df4["^GSPC"],color="red")
ax4.axvspan(Zone1_start,Zone1_end, color = "gray", alpha=0.3)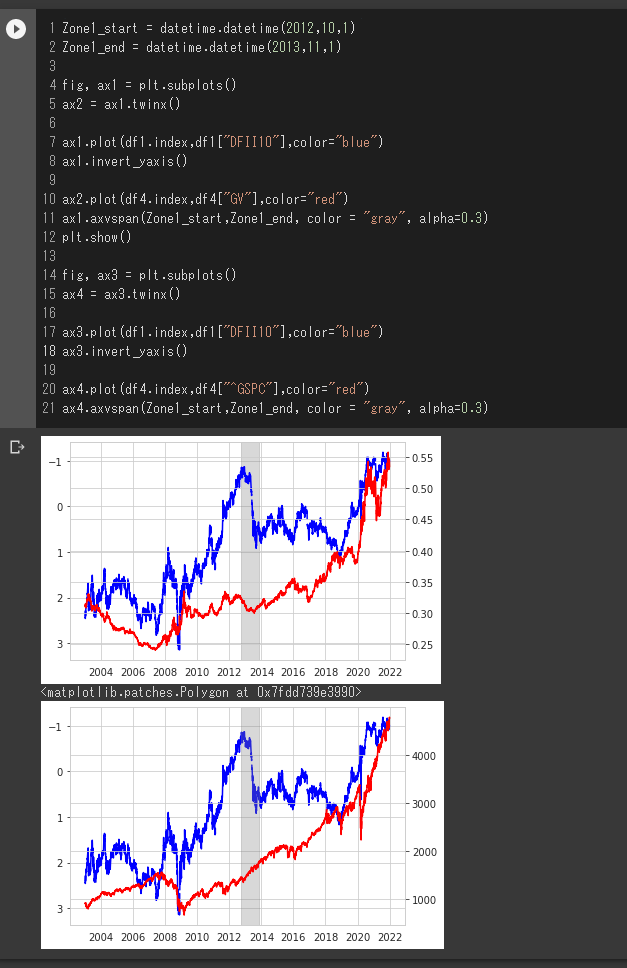
考察
切り取る区間によって関係があるようにも・ないようにも見えます。その時のマーケットのセンチメントや、何よりも企業業績を今度どのように見込んでいるのか、そういったものが影響してくるようにも思えます。
昨年3月コロナショックからの米国株の上昇が強かっただけに一旦の調整はあってもおかしくないところではありますし、インフレによる価格上昇を価格に転嫁できる企業と、そうでない企業の差は大きくなるようにも思えます。
個人的には米国株を外す選択肢はありませんので、引き続きある程度のレバレッジをかけながら大型株中心のインデックス投資、べた持ち投資を続けていく予定です。
2022/05/11 追記
ブログにTradingViewのウィジットを入れています。
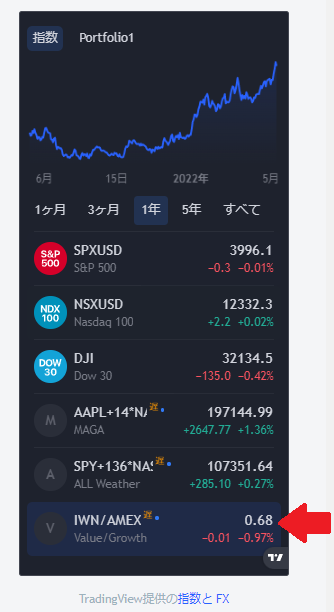
一番下IWN/AMEX (Value/Growth)の0.68という部分などをクリックすると現在の状態が確認できます。
2022/01/07 追記
Vanguard ETFを見ながら差分(比率)を見てみたいと思います。
参考にするETFは以下のリストからピックアップします。
ここで出てくるETFの種類については以下の記事などでも紹介しています。
私が思う現在の状況はARKKに代表されるハイパーグロース、短期売買の対象になっている小型株のグロースからの資金流出で、時価総額の大きな銘柄群のグロースには影響が無いわけではないが、まだ「壊れた」という状況でもないと思っています。
また、比率にして無次元での比較にすること、常にベンチマークと比較することで、状況の確認がしやすくなると思います。期間は5年とします。
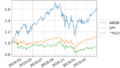
VBK:Small-Cap Growth ETF との比較
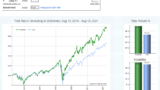
VOOG:S&P 500 Growth ETF との比較
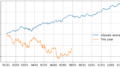
同じ”グロース”でも、S&P500比で結構な違いがあるように思えます。
上段を見る限り、コロナ後に急上昇し、昨年一月から S&P500 に劣後し続けているように見えます。
そして、それはARKKの動きと非常に近い動きになっているのが確認できるのではないかと思います。
”小型”グロースも結構いいところまで来ているように感じますが、反転は”当てる”ものではなく、”確認する”ものだと思うので、確認作業の時間が必要かと思います。
ディスクレーマー・投資に関する免責事項
情報の提供・作業代行を目的としており、投資勧誘を目的とするものではありません。
—
Python、投資に関する記事をご紹介します。








コメント