VIXが30を超えているときにS&P500を買っていると1年間保有していると+20%以上のパフォーマンスが得られます。ご存じでしたか?
VIX指数(CBOEボラティリティ指数)の水準を指標として、S&P500指数への投資や、戦術的・戦略的な立ち回りなどできたりするのでしょうか。実際のデータをもとに検証してみたいと思います。
本記事の目的
以下のようなヨーロッパ最大級の資産運用会社であるピクテ投信様が興味深い記事を書かれていました。

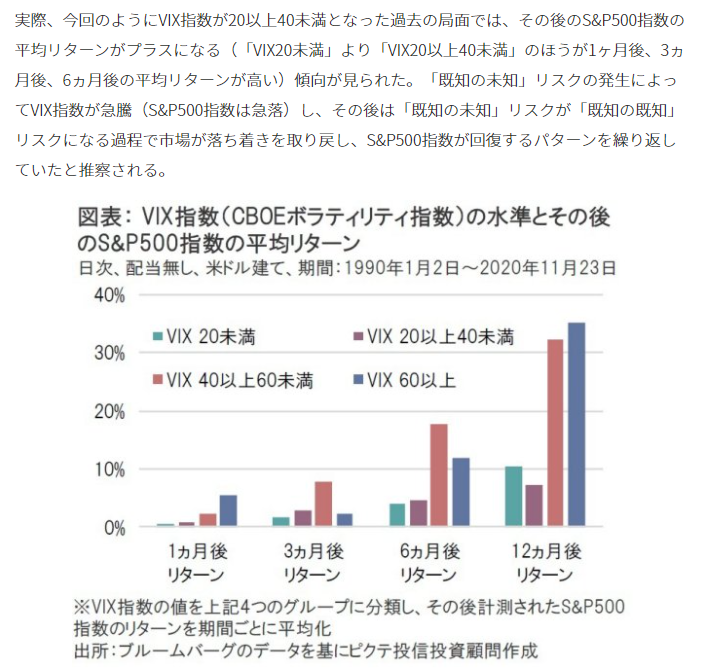
今回はこれを題材に、Pythonを用いて、実際にデータを取得・分析をしてみたいと思います。
データの取得
今回のデータはYahoo! US USのサイトから所得することとします。
データ端末のロールスロイスブルンバーグは当然使えませんので、今回も以前同様Pythonで自作です。
使用するツールはGoogle Colaboratoryのpythonを使いますので、無料で、簡単に行うことができます。Google Colaboratoryについては以前書いた記事をご参照いただければと思います。
また、似たような分析記事として
【コピペで動く!】VIXと米国株指数の関係 コロナ前・コロナ後 Pythonコードあり【違いをみつけろ!】
という記事を書いておりますので、興味ある方はそちらも参考にしてみてください。
実際のコードとやっていること
コードの前半部分は以下の通りです。
!pip install yfinance --upgrade --no-cache-dir
import datetime
import yfinance as yf
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
start = datetime.date(1990,1,1)
end = datetime.date.today()
codelist = ["^GSPC","^VIX"]
data2 = yf.download(codelist, start=start, end=end)["Adj Close"]
display(data2[codelist].head(2).append(data2[codelist].tail(2)))
plt.rcParams["font.size"] = 18
yyyymm=mdates.DateFormatter('%y/%m')
fig, (ax1 ,ax2 )= plt.subplots(2,1,figsize=(10,9),
gridspec_kw = {'height_ratios':[1, 1]},sharex=True)
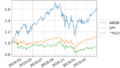
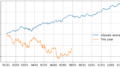
ax1.plot(data2.index,data2["^GSPC"],label="SPX")
ax1.legend(loc='center left', bbox_to_anchor=(1, 0.5), fontsize=18)
ax1.set_yscale('log')
ax1.grid(True)
ax2.plot(data2.index,data2["^VIX"],label="VIX")
ax2.legend(loc='center left', bbox_to_anchor=(1, 0.5), fontsize=18)
ax2.grid(True)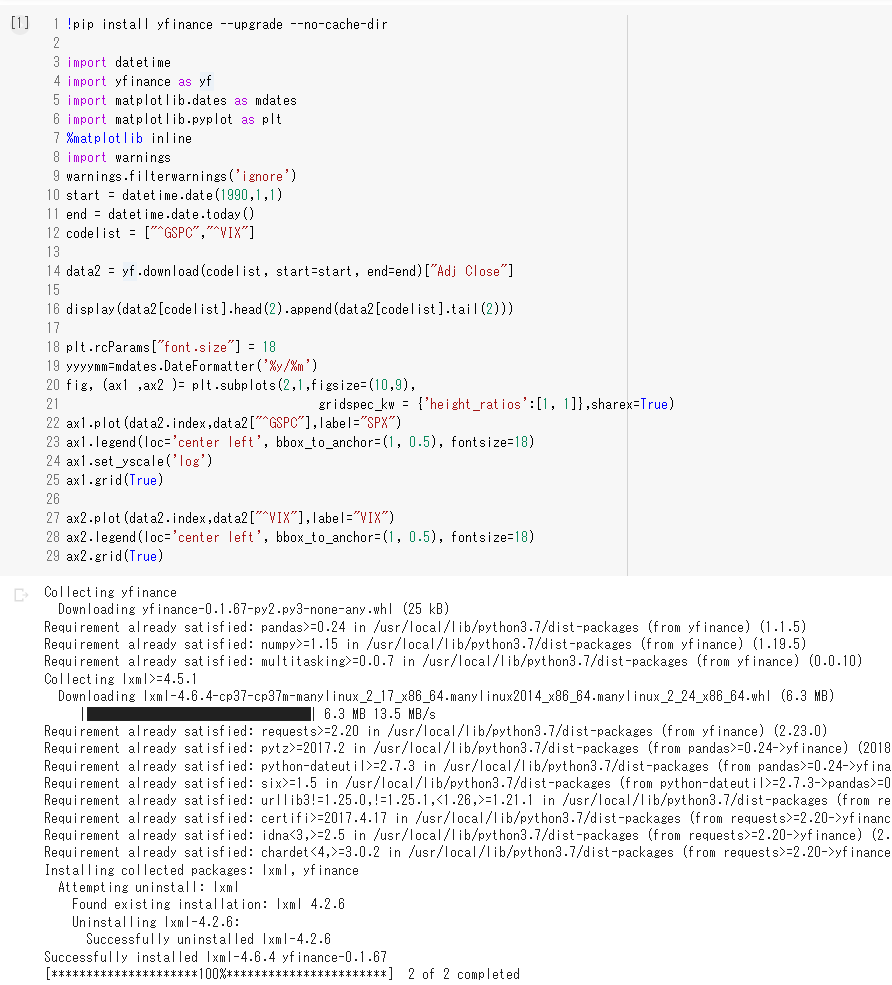
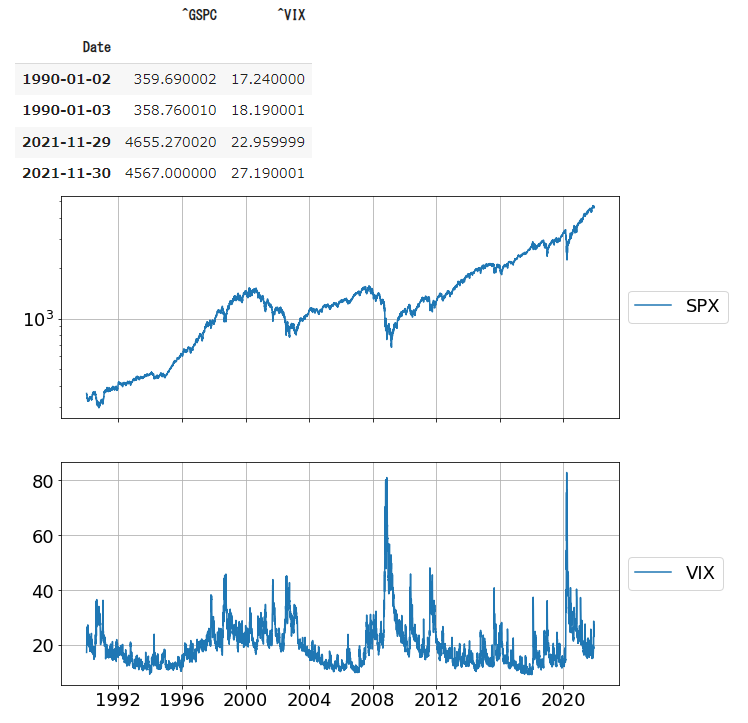
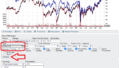
今回のデータ期間は1990年1月2日から2020年11月23日ということでしたので、データの取得開始日は 1990年1月2日 とし、取得期間の最終日は昨日2021年11月30日としました。データの種類は、日次のデータで配当なし、米ドル建てということですので、そのままのデータを使って分析できると思います。
また、最長で12ヵ月後のリターンとなりますので、約一年前までということもありますが、ある分だけデータを確認したいので、今回は取得できる分すべてを利用します。
S&P500は359から4567まで30年間で10倍以上になっていますので、ここでの表示は対数表示にしています。
分析・解析
データは準備できましたので、ここから分析・解析の開始になります。
今回は1ヶ月、3カ月、6カ月、12か月後ののリターンを求めることになりますので、一カ月を20営業日として、20日後、60日後、120日後、250日後のリターンとして分析を行うこととします。
コードは以下のようになります。
df_all=data2.copy()
df_all["R01"]=100*(df_all["^GSPC"].shift(-20)-df_all["^GSPC"])/df_all["^GSPC"]
df_all["R03"]=100*(df_all["^GSPC"].shift(-60)-df_all["^GSPC"])/df_all["^GSPC"]
df_all["R06"]=100*(df_all["^GSPC"].shift(-120)-df_all["^GSPC"])/df_all["^GSPC"]
df_all["R12"]=100*(df_all["^GSPC"].shift(-250)-df_all["^GSPC"])/df_all["^GSPC"]
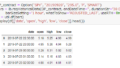
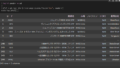
display(df_all.head(30))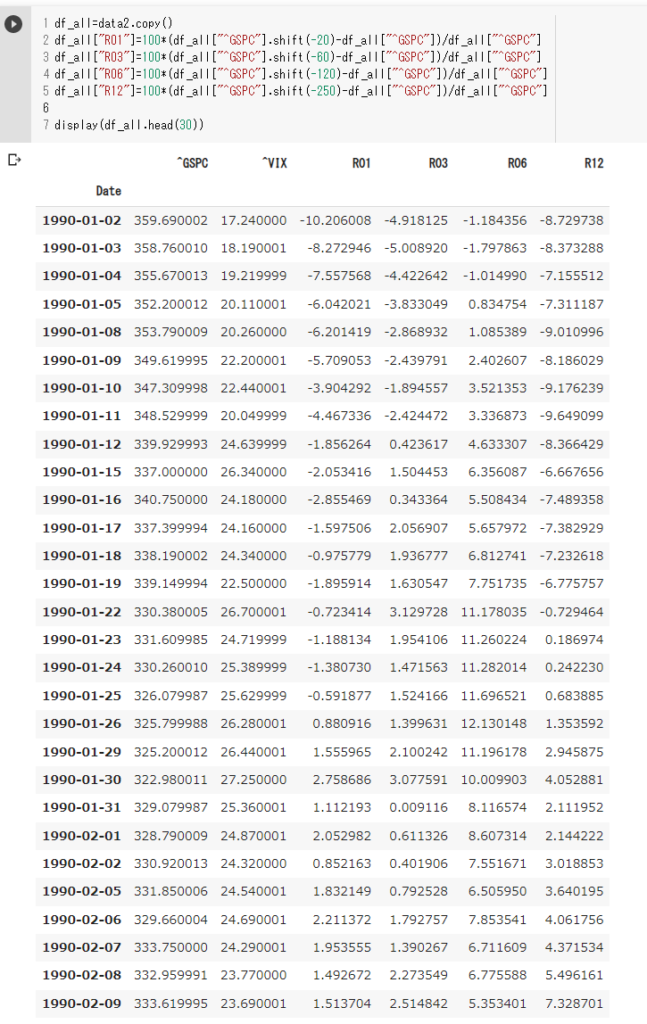
一カ月後(20日後)のリターンの計算方法としては、1990年1月2日の20日後1990年1月30日に株価は322.98を .shift関数を利用して計算します。
100*(322.98-359.69)/359.69=-10.20
正しく計算できていますし、それと同じことを 3カ月、6カ月、12か月後 でも行います。
平均をとる前に実際にはどのような分布なのか、プロットを行って確認します。
import seaborn as sns
plt.rc("legend", fontsize=18)
sns.jointplot("^VIX","R01",df_all,kind='reg',size=4)
plt.tick_params(axis='both', labelsize=18)
plt.grid(True)
sns.jointplot("^VIX","R03",df_all,kind='reg',size=4)
plt.tick_params(axis='both', labelsize=18)
plt.grid(True)
sns.jointplot("^VIX","R06",df_all,kind='reg',size=4)
plt.tick_params(axis='both', labelsize=18)
plt.grid(True)
sns.jointplot("^VIX","R12",df_all,kind='reg',size=4)
plt.tick_params(axis='both', labelsize=18)
plt.grid(True)
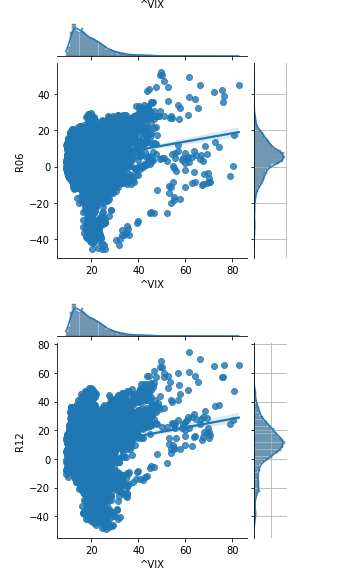
平均値だけでは見えてこない部分も散布図を見ると見えてくることもあります。
特に一カ月後リターンはVIXが40以上でもマイナス圏で推移していることも結構あることが見て取れます。その傾向は3カ月、6カ月でも同様でしょうか。
ただ、さすがに一年後はプラスになっていることが多いようです。
これからいえることは、VIXの高値から落ち着いても 3カ月前の価格、6カ月前の価格を越えられない場合があるので、 そういった短期ではない時間軸でも耐えられる資金管理も必要ということになると思います。
ゾーンによる S&P500指数の平均値 の計算
以下ではVIXのゾーンによるS&P500指数の平均値を求めます。
実際のコードは以下のようになります。
display(df_all[df_all["^VIX"]<20][["R01","R03","R06","R12"]].mean())
display(df_all[(df_all["^VIX"]>=20) & (df_all["^VIX"]<40)][["R01","R03","R06","R12"]].mean())
display(df_all[(df_all["^VIX"]>=40) & (df_all["^VIX"]<60)][["R01","R03","R06","R12"]].mean())
display(df_all[df_all["^VIX"]>60][["R01","R03","R06","R12"]].mean())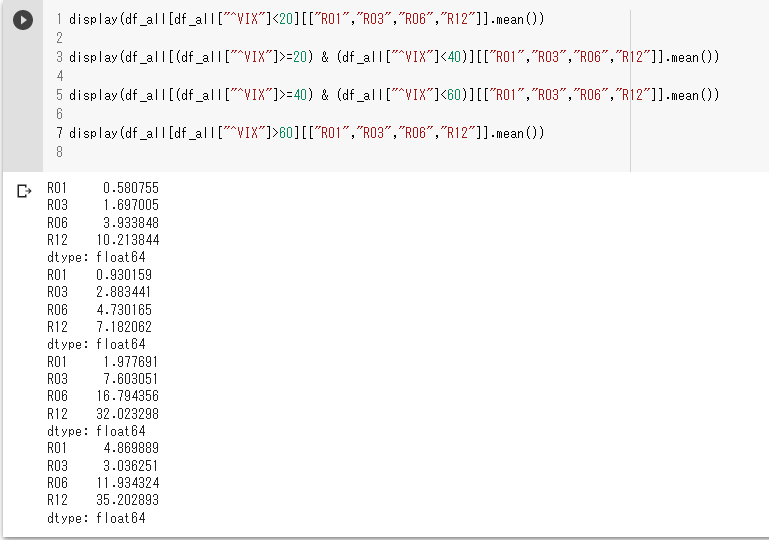
VIXの値におけるそれぞれのリターンの平均値を数値として出しています。
ただ、これだけだと、見にくいので、グラフとしてプロットします。
一旦グラフに日本語表記用のモジュールを読み込みます。
!pip install japanize-matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
棒グラフとして可視化します。
import numpy as np
x = np.array(['1ヵ月後の平均リターン', '3ヵ月後の平均リターン', '6ヵ月後の平均リターン', '12ヵ月後の平均リターン'])
x_position = np.arange(len(x))
R01_A=df_all[df_all["^VIX"]<20]["R01"].mean()
R01_B=df_all[(df_all["^VIX"]>=20) & (df_all["^VIX"]<40)]["R01"].mean()
R01_C=df_all[(df_all["^VIX"]>=40) & (df_all["^VIX"]<60)]["R01"].mean()
R01_D=df_all[df_all["^VIX"]>60]["R01"].mean()
R03_A=df_all[df_all["^VIX"]<20]["R03"].mean()
R03_B=df_all[(df_all["^VIX"]>=20) & (df_all["^VIX"]<40)]["R03"].mean()
R03_C=df_all[(df_all["^VIX"]>=40) & (df_all["^VIX"]<60)]["R03"].mean()
R03_D=df_all[df_all["^VIX"]>60]["R03"].mean()
R06_A=df_all[df_all["^VIX"]<20]["R06"].mean()
R06_B=df_all[(df_all["^VIX"]>=20) & (df_all["^VIX"]<40)]["R06"].mean()
R06_C=df_all[(df_all["^VIX"]>=40) & (df_all["^VIX"]<60)]["R06"].mean()
R06_D=df_all[df_all["^VIX"]>60]["R06"].mean()
R12_A=df_all[df_all["^VIX"]<20]["R12"].mean()
R12_B=df_all[(df_all["^VIX"]>=20) & (df_all["^VIX"]<40)]["R12"].mean()
R12_C=df_all[(df_all["^VIX"]>=40) & (df_all["^VIX"]<60)]["R12"].mean()
R12_D=df_all[df_all["^VIX"]>60]["R12"].mean()
y_Va = np.array([R01_A,R03_A,R06_A,R12_A])
y_Vb = np.array([R01_B,R03_B,R06_B,R12_B])
y_Vc = np.array([R01_C,R03_C,R06_C,R12_C])
y_Vd = np.array([R01_D,R03_D,R06_D,R12_D])
fig = plt.figure(figsize=(13,8))
ax = fig.add_subplot(1, 1, 1)
ax.bar(x_position, y_Va, width=0.2, label='VIX20未満')
ax.bar(x_position + 0.2, y_Vb, width=0.2, label='VIX20以上40未満')
ax.bar(x_position + 0.4, y_Vc, width=0.2, label='VIX40以上60未満')
ax.bar(x_position + 0.6, y_Vd, width=0.2, label='VIX60以上')
ax.legend()
ax.set_xticks(x_position + 0.2)
ax.set_xticklabels(x)
plt.grid()
plt.show()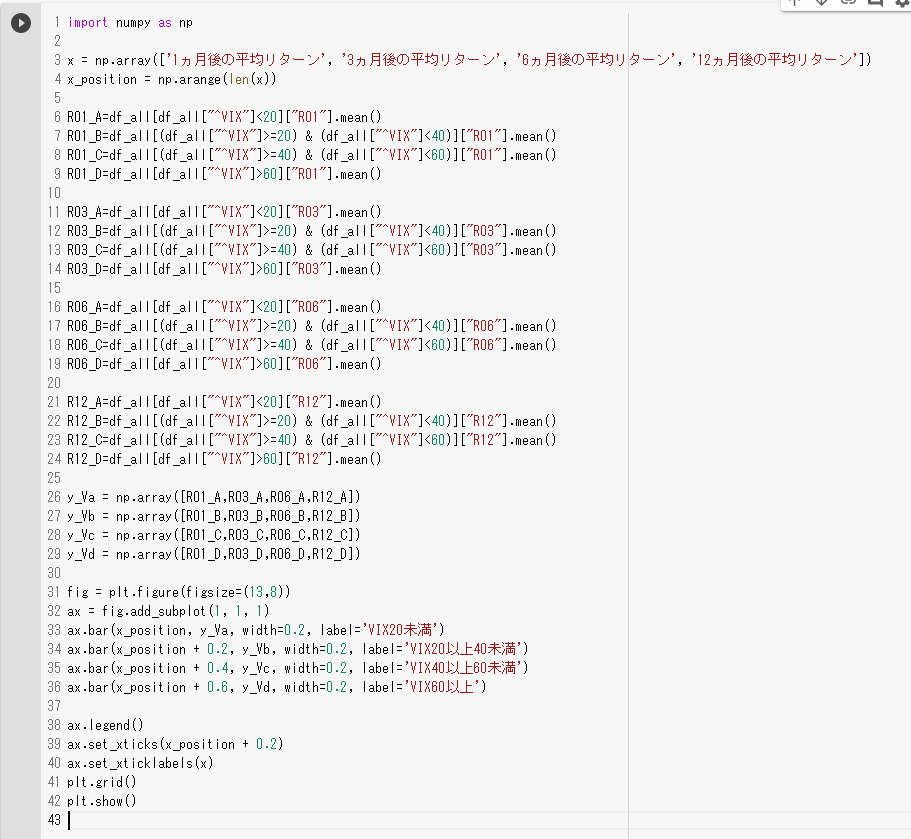
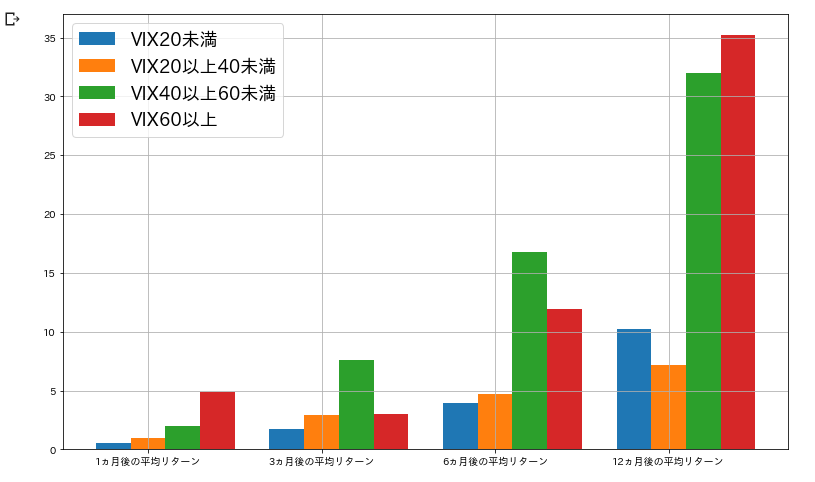
上記、紹介させていただいた記事に出ていたのとほぼ同じグラフを取得することができました。
また、棒グラフなどについては
【コピペで動く!】今年はどのようなアセットクラスがどのような値動きをしたのか、Pythonでデータを取得し、まとめてみた。あの話題の資産は年間でみるとこんなに上昇していた!
でも扱っております。
結論
・VIX(CBOEボラティリティ指数)が40以上というような極めて高い値をとる場合は、平均値としては半年から、一年後にはその時点からの投資で高いリターンを得られる可能性がある
・VIX(CBOEボラティリティ指数)が40以上であっても一カ月といった比較的短いスパンでは その時点からの投資であっても、高いリターンとならない場合もある
・上記結果はあくまで平均値の結果であり、場合によってはマイナスとなる場合もかつてはあった
というものでしょうか。もちろん、これ以外についてもいえることはあると思いますが、是非、ご自身で分析等してみて新しい発見をしていただければと思います。
追記
以下のようなTweetを拝見しました。
実際のその通りなのか、2022/05/04時点でのデータで確認してみました。
コード自体は上記の物を利用して、追加分は以下のようになります。
display(df_all[df_all["^VIX"]>30][["R01","R03","R06","R12"]].mean())
実際に+23%(R12の部分)、期間にもよると思いますが、+22%というのは間違いないようです。
また、VIXの値30以上とそれ以下で相関を見てみます。
df_VIX30=df_all.copy()
df_VIX30['VIX30']="DOWN"
df_VIX30.loc[df_VIX30["^VIX"] >= 30, 'VIX30'] ="UP"
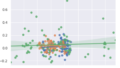
g = sns.lmplot(x="^VIX", y="R12", hue="VIX30", data=df_VIX30,height=5, aspect=1.5, line_kws={'color': 'red'})
plt.grid(True)
plt.show()
g = sns.lmplot(x="^VIX", y="R12", data=df_all,height=5, aspect=1.5, line_kws={'color': 'red'})
plt.tick_params(axis='both', labelsize=18)
plt.grid(True)
plt.show()
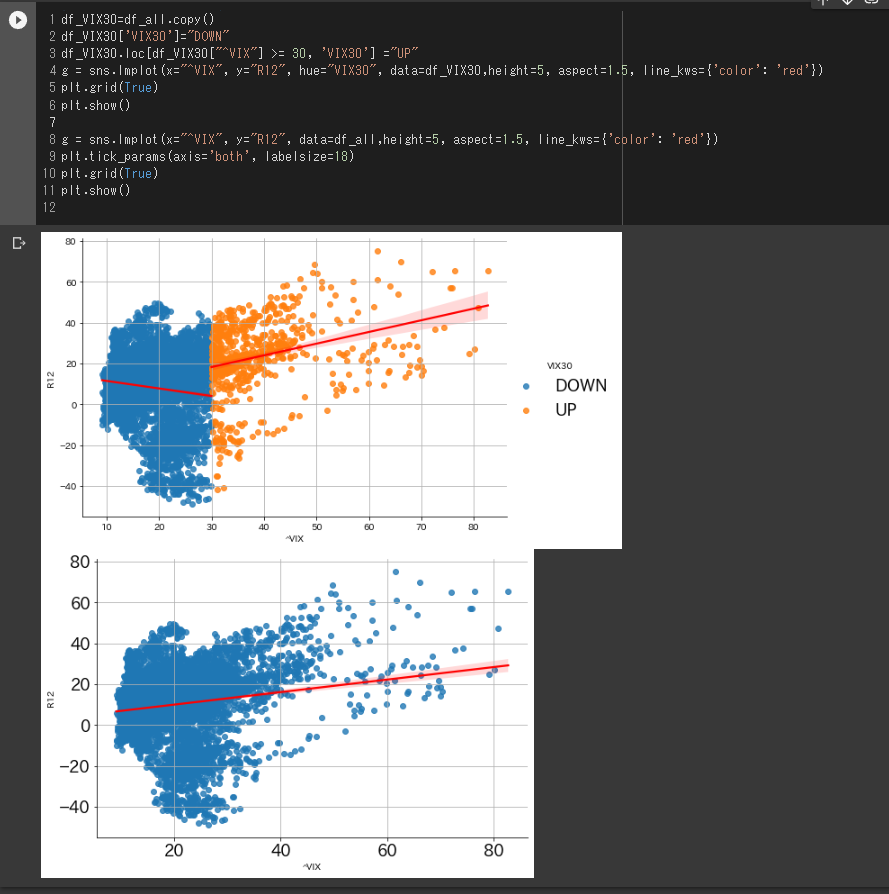
VIX値によるリターンの相関は違うようですね。色分けしている部分などについては
の記事をご参照いただければと思います。
VIXによる相場の判定、リターンの特性についてはいろいろ研究の余地がありそうです。
興味のある方はいろいろやってみてはいかがでしょうか。
ディスクレーマー
投資に関する免責事項情報の提供・作業代行を目的としており、投資勧誘を目的とするものではありません。
[Past performance is no guarantee of future results]
---
関連記事を紹介します。
VIXに関するダッシュボード
投資に関する記事をご紹介します。










コメント