ビットコインの値動きを題材に対数正規分布をもとにした分析を行い、考え方や実際のプラグラムのコードを表記などを行うことをめざします。
また、その工程でCSVファイルの読み込み、文字列となっているデータを数値データや日付データに変換するなど、データの前処理についてもご紹介します。
乱暴な表現をさせてもらえればデータサイエンティストの仕事の8割がたは前処理、データ取得だったりもしますので、そのあたりのヒントになればと思います。
本記事を書いた理由
クリスマスの時期でもありDFさんが以下のようなツイートをされていました。
e(自然対数の底)とかLogというのがなかなかなかなかおしゃれですね。
今まで【コピペで動く!】の記事では変化の比率を計算するpct_change関数を使っていたのですが、本格的な分析手順、作法(!?)としても、対数を用いた記事も書いておいた方がいいかなと思い今回の記事を書くことにしました。
私も実務系であり理論派ではないこと、サラリーマントレーダーとして、ビットコインなど主戦場である部分にどこまで情報提供できるの、、という物はありますが、できる範囲で書いてみたいと思います。
対数正規分布の考え方
価格が10倍(それ以上)など強烈に上昇する場合や、ボラティリティが極めて大きな場合はLog対数で分析する必要があります。具体的な例としては株価が100だったものが50になり、再度100に戻った場合を考えます。
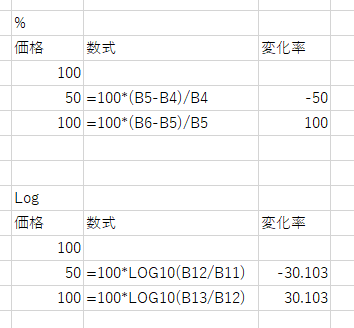
通常のパーセントで考えると-50%下落し、戻る場合は2倍になるので100%の上昇ということになります。
ただこの視点では、「株価などの経済のデータはランダムに変動しているとみなす」という経済理論、そして確率分布の視点から考えると問題があるということなります。
ですが、これを対数の分析にすると、下段のように価格が半分になる確率と、2倍になる確率を公平に判断できるということになります。
難しい場合は、”分析作法”としてその手順に従ってください、ということになります。
もう少し難しく言うと、時点tにおける資産価格Stの確率微分方程式、ブラウン運動のような不確実な項(ドリフト項)を仮定すると瞬間的な収益率が正規分布に従うとき、資産価格は対数正規分布に従うということになります。
さらに言えば、 今回は対数正規分布を仮定していますが、実際のビットコインや日経平均株価をはじめ株価などの価格の前日比は対数正規分布と比べると裾が厚い、つまり極めて大きな・小さい値が起こるべき分布の世界だったりしますが、それでは分析できないということになりますので、大きな変動部分は、正規分布の例外(ファットテール)として実務部分でフォローアップするというのが現在のファイナンス理論全般で多く行われている対応ということになります。
https://www.eco.nihon-u.ac.jp/center/industry/publication/research/pdf/41/41_03.pdf上記のような論文において
リスク資産価格の収益率の分布は正規分布に比べて裾が厚いことが広く知られており,リスク資産価格収益率のボラティリティは市場の変化に応じて時間を通じて変動している.このような特徴を持つ時系列データは,通常,GARCH(Generalized Autoregressive Conditional Heteroskedasticity)モデル,EGARCH (Exponential GARCH)モデルなどの ARCH 型モデル 1)や確率的ボラティリティ変動(Stochastic Volatility)モデル 2)などで定式化されることが多く,リスク資産価格分析に関して
https://www.eco.nihon-u.ac.jp/center/industry/publication/research/pdf/41/41_03.pdf
頻繁に利用されている.また,リスク資産の中でも株価収益率や外国為替レート変化率の分布は歪んでいて,左右非対称であることが多くの実証研究で示されている.そのため,このような現象を捉えるには,平均が異なる分布から構成される混合分布による定式化が考えられ,里吉・三井(2013)では混合正規分布と混合 t 分布を用いて,日経平均の分析を行なっている.
とあったりします。このあたりの導入部分をご紹介できればと思います。
データの取得
こちらの記事を参考にしながらYahoo-USのサイトからビットコイン (BTC-USD) の価格を取得しようかと思いました。
【コピペで動く!】今年はどのようなアセットクラスがどのような値動きをしたのか、Pythonでデータを取得し、まとめてみた。あの話題の資産は年間でみるとこんなに上昇していた!(追記:直近1カ月もチャートで出せるようにしました)
ただ、Yahoo-USのビットコイン(BTC-USD)のデータ取得可能期間は2017年11月からのようです。
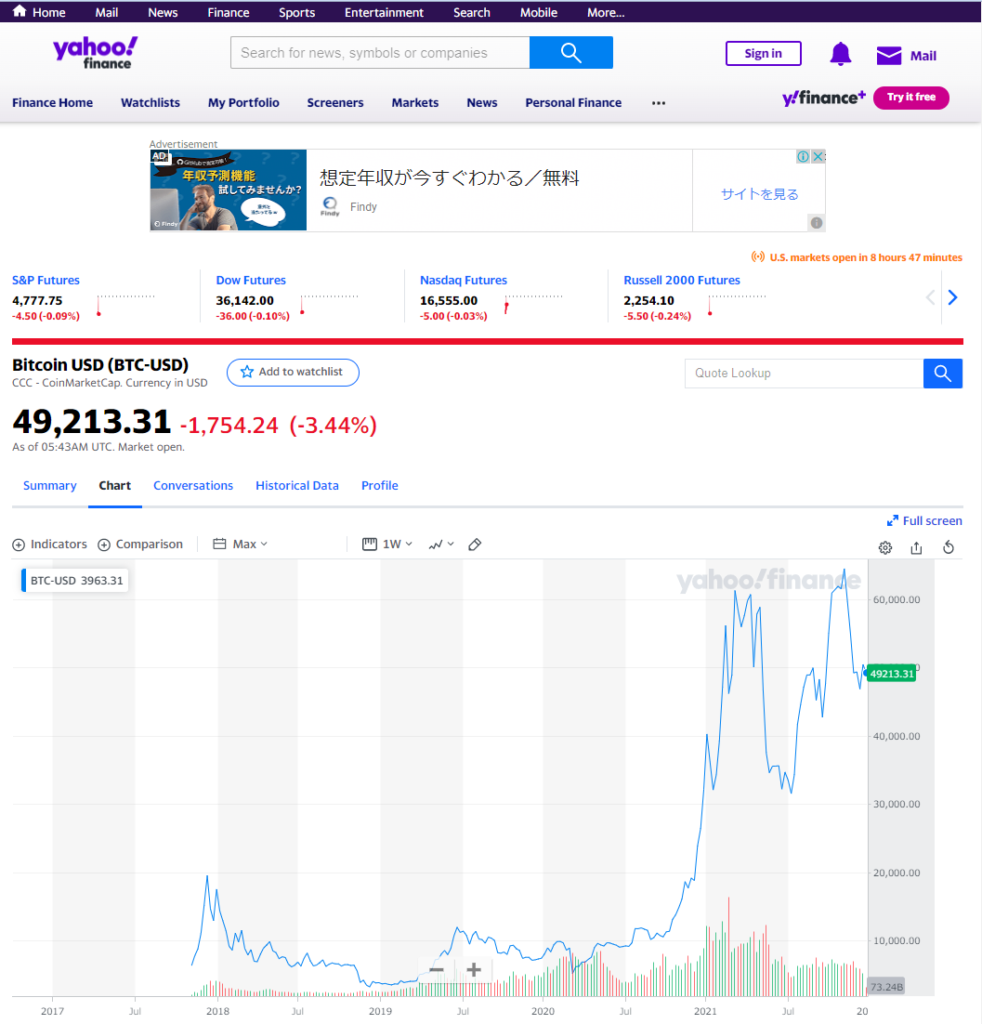
さすがにこのだと期間が短いと思いますので、今回は investing.com 様のデータを利用したいと思います。

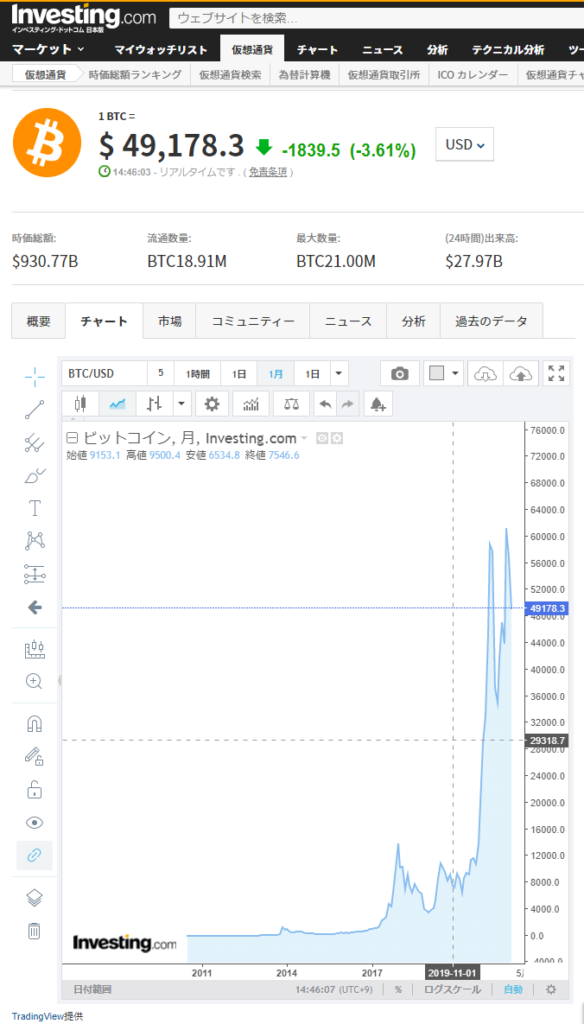
データ的には2010年8月からあり、そのデータをCSVで出力できるようです。
実際の出力は「過去のデータ」タブから「時間枠を月間」、「期間の設定」の開始日を2010年から選択すると2010年8月からデータが取得できます。
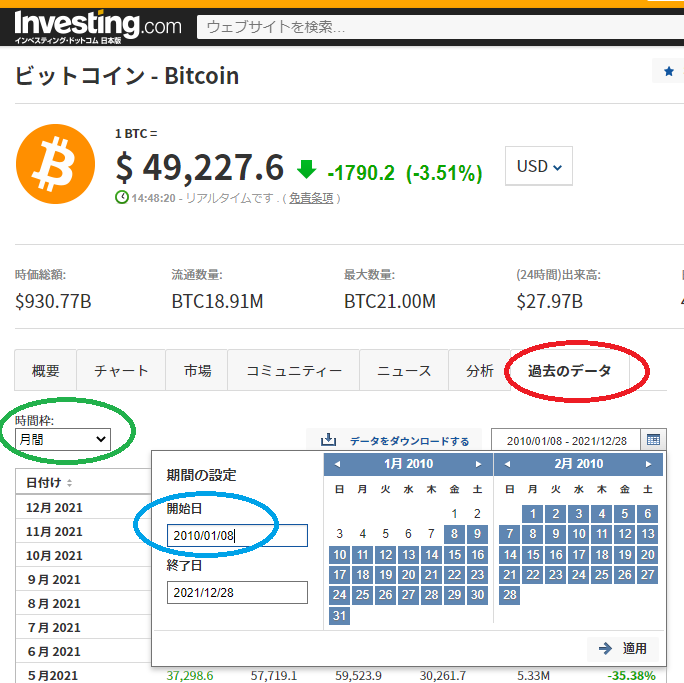
このデータをCSVに出力するには「データをダウンロードする」を選択する必要があります。
ただ、ログインする必要があります。無料でアカウントは作れますので、GoogleアカウントやFacebookアカウントなどでログインをして下さい。
実際ダウンロードすると、Windowsの場合はダウンロードフォルダに「Bitcoin – ビットコイン過去データ – Investing.com.csv」といった名前でファイルが作成されます。
Pythonによる分析
今回も以前同様使用するツールはGoogle Colaboratoryのpythonを使います。無料で、簡単に行うことができます。Google Colaboratory自体については以前書いた記事をご参照いただければと思います。
実際のコードとやっていること
CSVファイルの読み込み、 アクセスなどはこの記事などを参考にいただければと思います。
【コピペで動く!】Pythonで1.5GBのcsvファイル読み込み高速化:1分5秒⇒4秒程度 DASK , pickle (Pythonコードあり)
今回は事前に Investing.com から出力したCSVファイルを Google Colaboratory に読み込みます。
まず、今回使うファイルをGoogle Colaboratoryにアップロードします。
簡単なのは左側のタブの中にあるファイルを選んでいただき、アップロードのボタンの押すと、アップロードするファイルを選べますので、そこで読み込み等に使いたいファイルを選択します。
今回は ”Bitcoin – ビットコイン過去データ – Investing.com.csv” というファイルを私はアップロードしました。
このファイルの状況をまず、確認します。
import os
print(os.path.getsize("Bitcoin - ビットコイン過去データ - Investing.com.csv"))
9Kのファイルということでしょうか。月足ですので、非常に小さいです。長い期間での日足、さらには一時間足、分足となるとテキストデータといえども巨大なファイルになることもあります。
データのロード
import pandas as pd
df = pd.read_csv("Bitcoin - ビットコイン過去データ - Investing.com.csv")
display(df,df.info())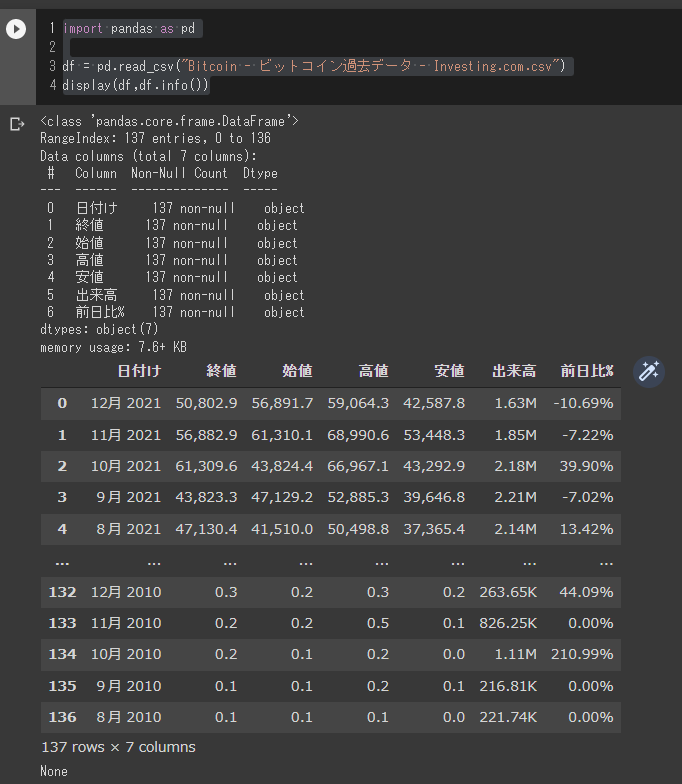
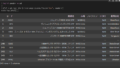
Webの画面で出ていたままのデータが読み込めていることが分かります。
ただし、日付が”m月YYYY”という書式なこと、スペースもあれば、全角数字という”前処理”を必要がありそうです。
また、終値も カンマ(,)が入っていたりしますし、データ自体も日付の降順になっていたりします。
データ端末のロールスロイス、ブルームバーグが欲しいですが、ないものは仕方ないので、このあたりを解析前の前処理で処理します。
文字列データを日付、数値データへ変換
!pip install mojimoji
import mojimoji
import matplotlib.pyplot as plt
df['DATA_MOD1'] = df['日付け'].apply(lambda s: mojimoji.zen_to_han(s))
df['DATA_MOD1'] = df['DATA_MOD1'].str.replace(' ', '')
df['date'] =pd.to_datetime(df['DATA_MOD1'], format='%m月%Y')
df=df.set_index("date")
df=df.sort_index()
df["close"]=pd.to_numeric(df["終値"].str.replace(',',''))
df["pct"]=df["close"].pct_change()
plt.plot(df.index,df["close"])
display(df,df.info())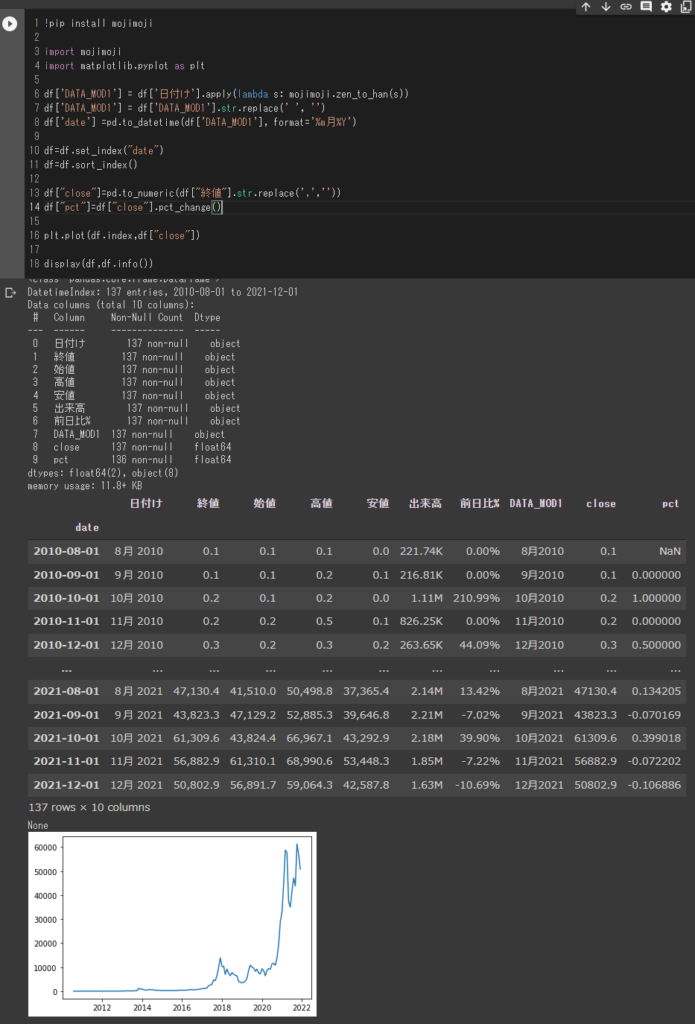
mojimoji というモジュールで全角文字を半角文字に変更しますので、インストールします。
「日付け」列の全角文字を変更したのち、「月」の後ろにある空白(スペース)を削除します。
その処理を行った列を Datetime であると指定することでただのテキストデータだったものを時系列データに変換し、その列をインデックス化、昇順に並べ替えます。
次のステップでは終値もカンマのあるテキストデータですので、カンマを削除したのち、数値データへ変換します。合わせて、パーセントでの変化率を計算しておきます。
QC(クオリティチェック)として、終値ベースでの価格のプロットと、「前日比%」列と今回計算した「pct」列の値が同じになっていることを確認します。
価格が0.1が0.2になった時の変化率は問題がありありそうですが、下段5つのデータは13.42%から-10.69%まで問題ないように見えますので、データ的には問題ないと思われます。
ただ、2010/9月にビットコイン(BTC-USD)が1ドルですらなかった、少額でも持っていれば、、、というのはここでは取り上げません。😢
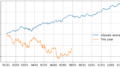
累積和・累積積
累積和・累積積の違いをプロットして可視化しておきます。
df_pct=df[["close","前日比%","pct"]].copy()
display(df_pct)
df_pct["close"].plot(figsize=(8,6),fontsize=18)
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5), fontsize=18)
plt.show()
(1+df_pct["pct"]).cumprod().plot(figsize=(8,6),fontsize=18)
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5), fontsize=18)
plt.show()
df_pct["pct"].cumsum().plot(figsize=(8,6),fontsize=18)
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5), fontsize=18)
plt.show()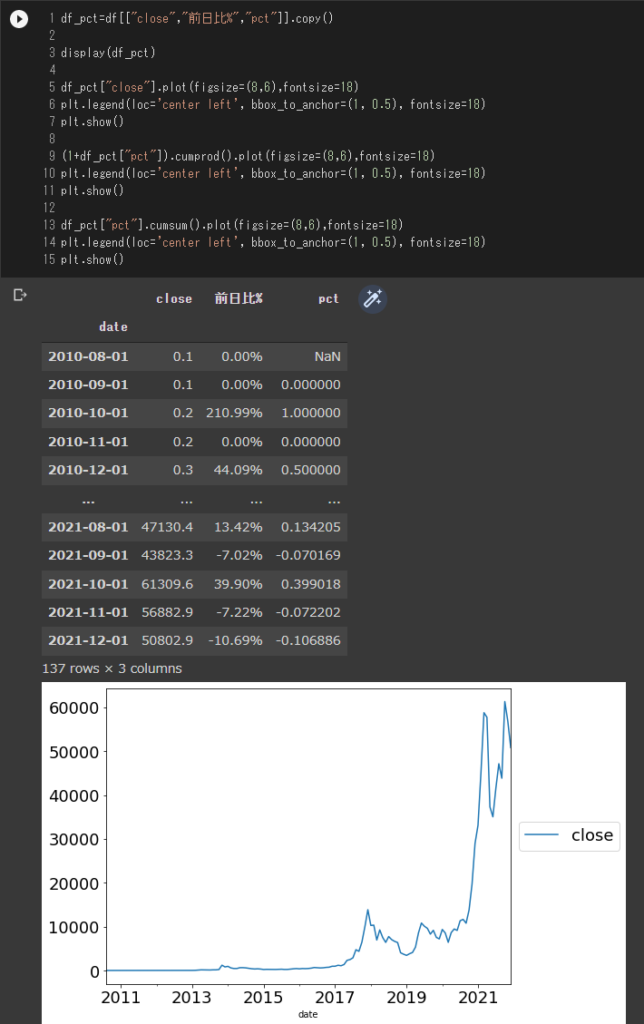
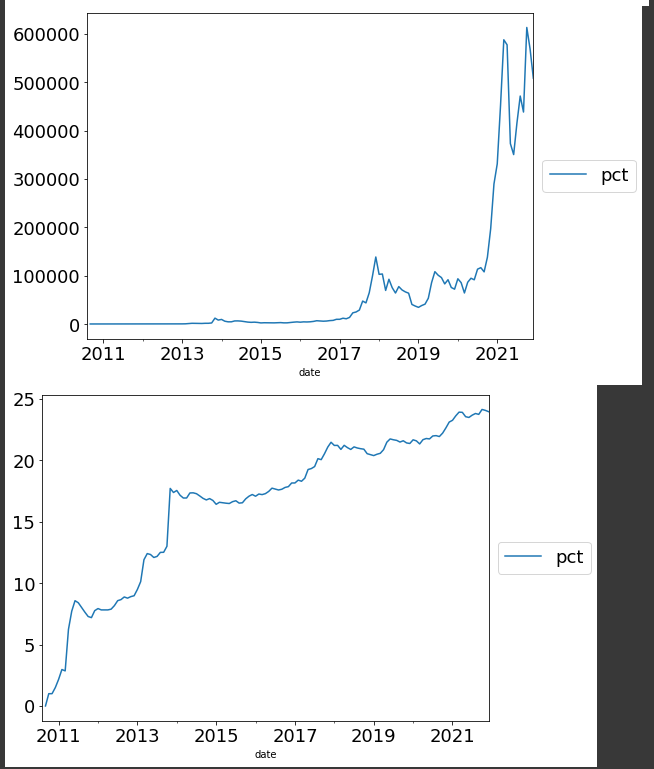
複利の効果ではないですが、元本に対して加速度的に上昇していくものが 累積積 、資産価格では見て取れます。単純な変化率の総和ではないことが確認できると思います。
seaborn-analyzer によるデータの可視化
今回は既存のデータ可視化ツールを使ってデータの分布などの可視化を行います。
詳細についてはこちらをご覧ください。


非常に便利なツールがあるものです。作っていただいた方に感謝です。
QQプロットで正規分布からのはずれを可視化したり、ヒストグラムで分布形状を可視化したりします。
単純なパーセント変化率でのヒストグラムとQQプロットは以下のようになります。
!pip install seaborn-analyzer
import numpy as np
import seaborn as sns
from seaborn_analyzer import hist
display(df_pct.describe())
hist.plot_normality(df_pct["pct"].dropna(),norm_hist=False, rounddigit=5)
plt.show()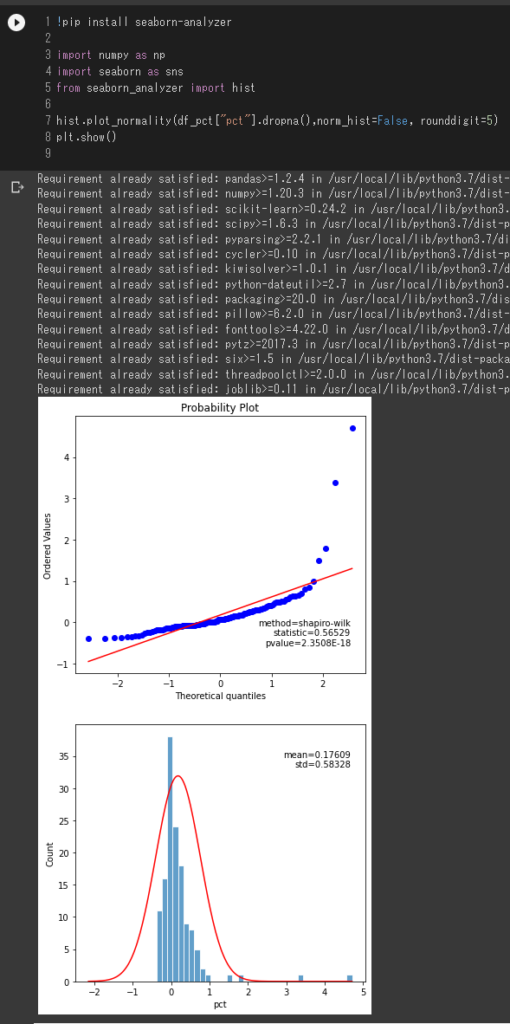
ヒストグラムについて上昇しているということもありますが、右にずれているようにみえますし、QQプロットについても直線に近いほど正規性が高いという観点からみるともう一工夫必要かな、、という気がします。
また、このツールでは各種確率分布のフィッティングすることもできます。
all_params, all_scores = hist.fit_dist(df_pct["pct"].dropna(), dist=['norm', 'lognorm'])
plt.show()
all_params, all_scores = hist.fit_dist(df_pct["pct"].dropna(), dist=['norm', 'lognorm','t'])
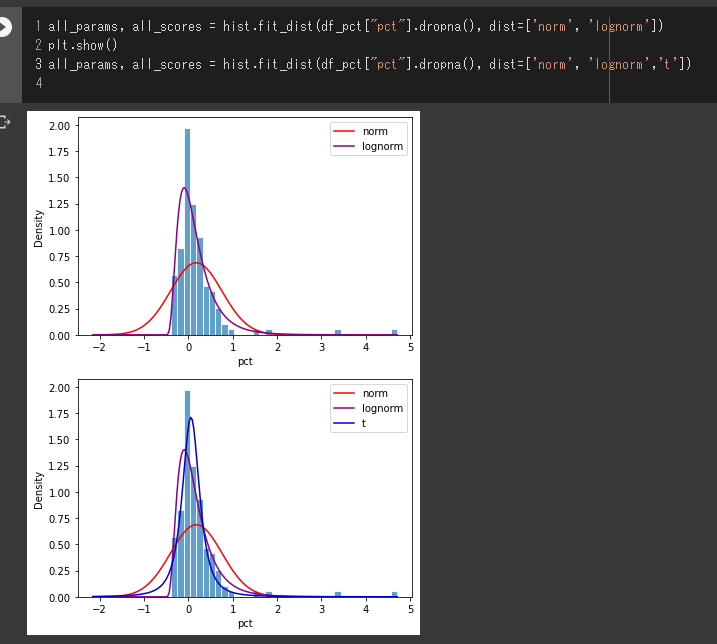
正規分布は使えないということはわかると思います。
それでは、対数で分析した場合はどうなのでしょうか?見ていきたいと思います。
df_pct["log"]=np.log10(df_pct["close"]/df_pct["close"].shift(1))
display(df_pct.describe())
hist.plot_normality(df_pct["log"].dropna(),norm_hist=False, rounddigit=5)
plt.show()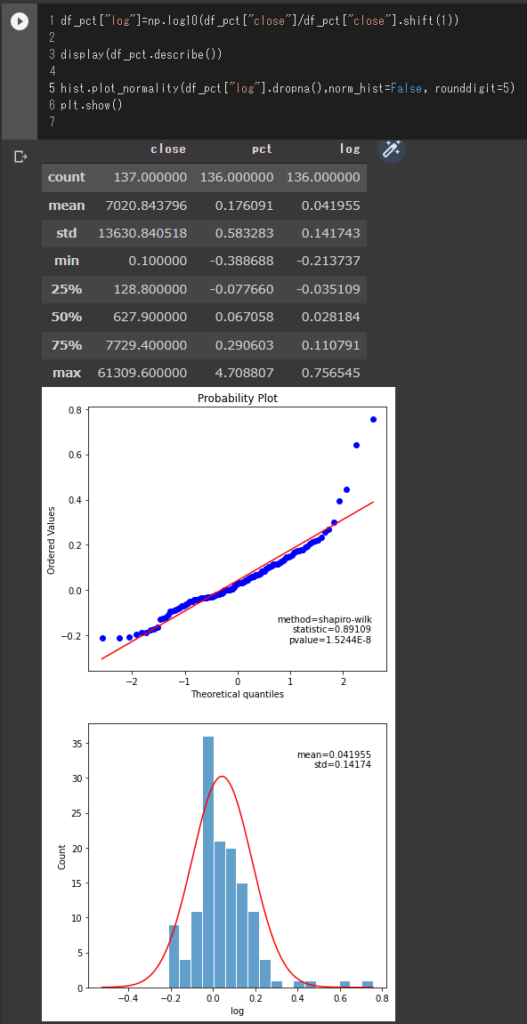
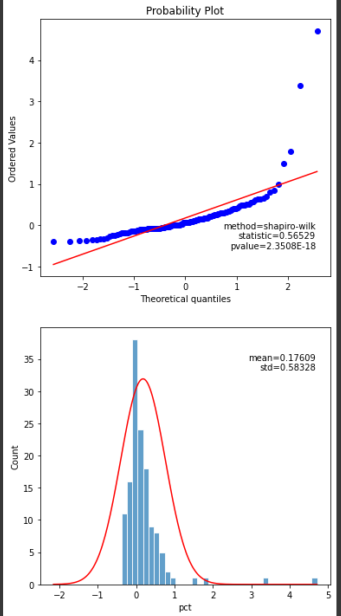
QQプロットは完全に直線にフィットしているとはいいがたいですが、先ほどよりは良くなっているように見えます。また、ヒストグラムも-0.2から0.2である程度対称っぽく見える気もします。ただ、 リスク資産価格の収益率の分布は正規分布に比べて裾が厚いという部分は見て取れると思います。
各種確率分布のフィッティング は以下のようになります。
all_params, all_scores = hist.fit_dist(df_pct["log"].dropna(), dist=['norm', 'lognorm'])
plt.show()
all_params, all_scores = hist.fit_dist(df_pct["log"].dropna(), dist=['norm', 'lognorm','t'])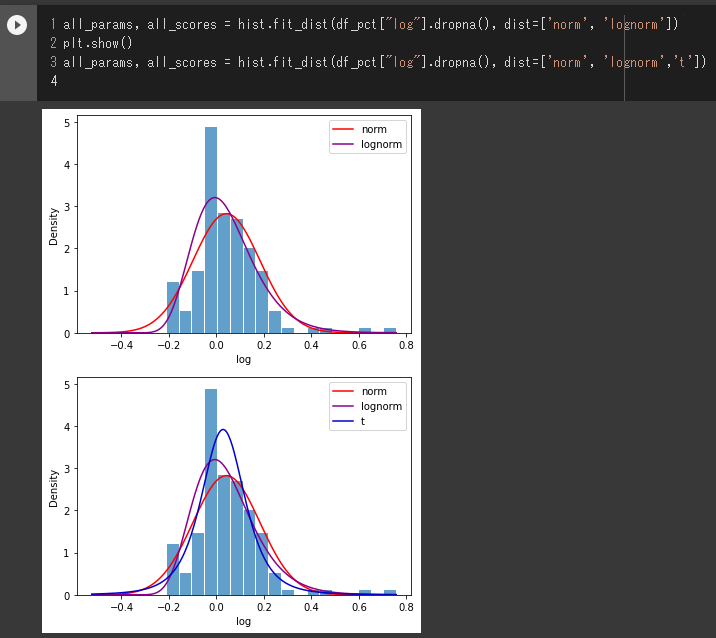
上で引用した論文でもありましたが、対数正規分布、t分布、 大きな変動部分は、正規分布の例外(ファットテール)として実務部分でフォローアップするというようなアプローチが現実的な手立てとなっているようです。
今回は月足での分析でしたが、週足で行った場合や日足などの分析だとどうなのか。
検証対象をS&P500などの株価指数やGOLDといったコモディティ、TLTといった債券ETFなど、いろいろ調べてみると面白いことが分かるかもしれません。
興味のある方は自身で調べられてはいかがでしょうか?
最後まで読んでいただき、大変ありがとうございました。
—
Python、投資に関する記事をご紹介します。










コメント