債券利回りが反転上昇の傾向を示しています。その上昇におびえるかのように株価指数は調整の様相ですが、過去の債券利回り上昇時にどのような動きがあったのか、確認してみたいと思います。
2022/03/30追記:現在の米国債券関連のチャートを追加します。
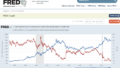
Treasury yield curve flattening/inversion signals/Constant Maturity
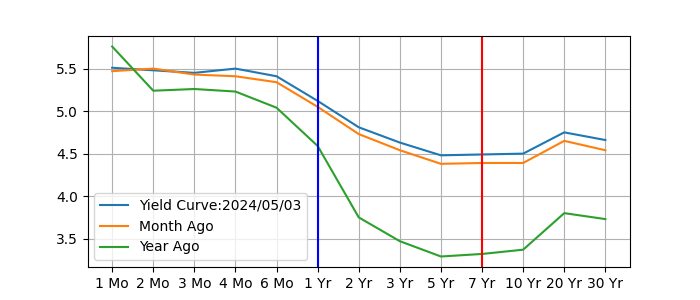
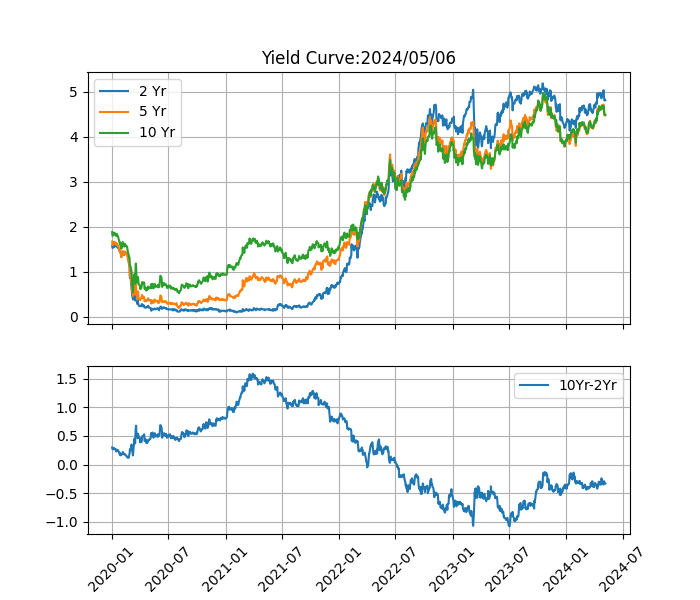
米国債10年と2年の利回り差
また、債券についてより基本的なことから知りたいという方には私の記事ではありませんが、以下の記事をご参考にいただければと思います。非常にわかりやすく書かれていると思います。

追記終了
データの取得
今回のデYahoo! US USのサイトから3種類のデータを取得します。
Treasury Yield 10 Years (^TNX) : アメリカ 10年債券利回り
S&P 500 (^GSPC)
NASDAQ Composite (^IXIC)
確認できる範囲では1985年あたりから、データが所得できるようです。それらがどのような値動きをしたのか、過去の債券利回り上昇時にS&P500指数やナスダック指数はどのような値動きをしたのか、確認してみたいと思います。
以前こちらで使用したでデータ取得もとであるセントルイス連銀では株価指数の取得可能期間がS&P500は2012年からと、若干データ数が少ないように感じたいので、今回はYahoo! USのデータソースを利用することにしました。
Pythonによる分析
今回も以前同様使用するツールはGoogle Colaboratoryのpythonを使います。無料で、簡単に行うことができます。Google Colaboratoryについては以前書いた記事をご参照いただければと思います。
実際のコードとやっていること
コードは以下の通りです。
!pip install yfinance --upgrade --no-cache-dir
import datetime
import yfinance as yf
import matplotlib.pyplot as plt
import pandas as pd
pd.options.display.float_format = '{:.4f}'.format
start_D="1985-1-1"
end_D = datetime.date.today()
codelist = ["^IXIC","^GSPC","^TNX"]
data2 = yf.download(codelist, start=start_D, end=end_D)["Adj Close"]
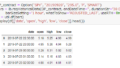
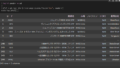
display(data2.head().append(data2.tail()))
display(data2.describe())
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax2 = ax1.twinx()
ax1.plot(data2.index,data2["^IXIC"],label="NASDAQ Composite",color="blue")
ax1.plot(data2.index,data2["^GSPC"],label="SP500",color="orange")
ax2.plot(data2.index,data2["^TNX"],label="Treasury Yield 10 Years",color="red")
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax1.legend(h1 + h2, l1 + l2,loc='center left', bbox_to_anchor=(1, 0.5), fontsize=18)
ax3.grid()
plt.show()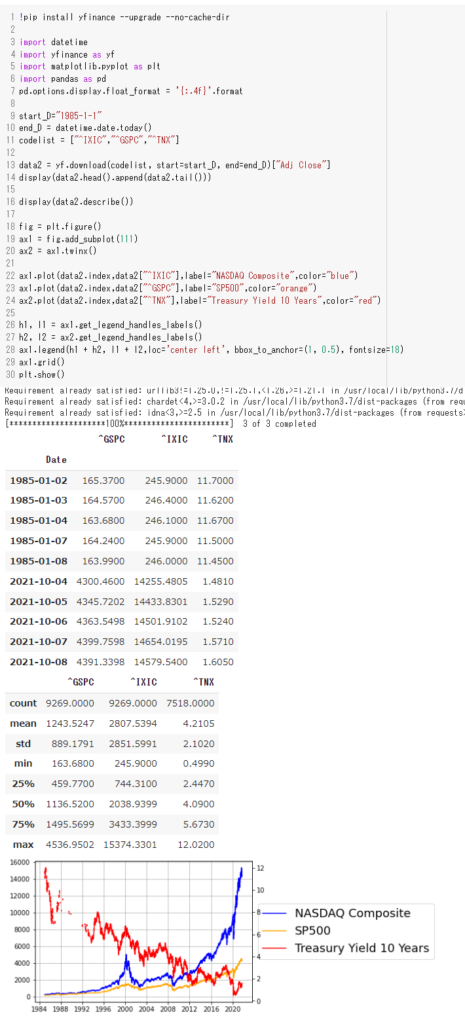
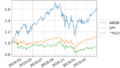
データの取得と各列の要約統計量を取得し、まずはそのままの値を右軸に債券利回り、左軸に株価指数のメモリとして、出力します。
まず驚きはS&P500は1985年には165だったものが現在4391と、約26倍になっていることと、ナスダックにいたっては245が14579と約60倍にもなっていることです。
十分、インフレです。それ以上は何も言いますまい。。。
早く始めた方が有利でしたね、、(恐らく今も、有利です。)
アメリカ 10年債券利回りについては12から1.6まで落ちているようです。無リスクの資産運用先としての米国債という物がありますので、運用利回りが下がると、それを補うようにリターンを必要とする資金がいろいろ運用先を求めて動いているという事もあると思います。
データ分析の前処理
今回は株価指数が非常に大きな変化をしています。基本的には10倍以上になっていたりするので、本来は対数処理など、データ分析の前処理をする必要があります。
データの差分や無次元化、株価などであれば対数正規分布への処理など、いろいろありますが、ここは簡便にパーセント処理した状態での解析とします。
興味がある人、さらに言えば、より精密な分析をしたい方はそのあたり、ご自身で行ってみてください。
今回はデータの空白地帯が終わった1992年以降で日次での変化率で分析を行っていきます。
df1=data2["1992-1-1":].pct_change().copy()
display(df1.describe())
fig = plt.figure()
ax3 = fig.add_subplot(111)
ax4 = ax3.twinx()
ax3.plot(df1.index,(1+df1["^IXIC"]).cumprod(),label="NASDAQ Composite",color="blue")
ax3.plot(df1.index,(1+df1["^GSPC"]).cumprod(),label="SP500",color="orange")
ax4.plot(df1.index,(1+df1["^TNX"]).cumprod(),label="Treasury Yield 10 Years",color="red")
h1, l1 = ax3.get_legend_handles_labels()
h2, l2 = ax4.get_legend_handles_labels()
ax3.legend(h1 + h2, l1 + l2,loc='center left', bbox_to_anchor=(1, 0.5), fontsize=18)
ax3.grid()
plt.show()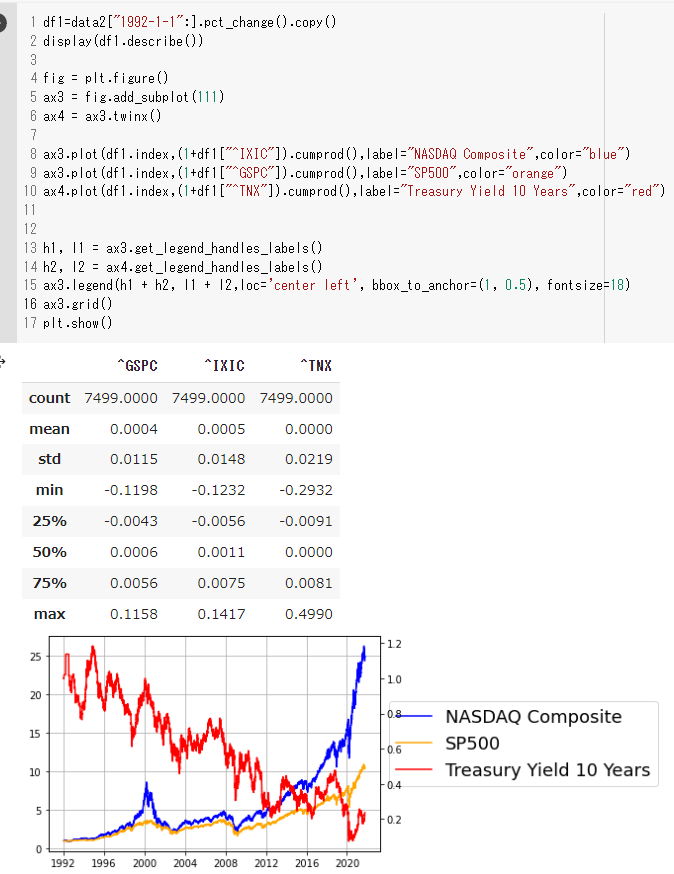
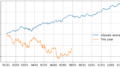
ここでは累積積を算出して実際の価格推移に変更します。累積積とは1番目の要素 * 2番目の要素 * 三番目の要素 * … と和が累積されていく計算のことです。
同じ形のチャートになっていることが見て取れると思います。
クロスプロット
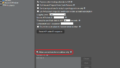
横軸X軸を債券利回りの日次の変化率、縦軸Y軸を株価指数の変化率としてクロスプロットを行います。
import seaborn as sns
sns.set_style('whitegrid')
import warnings
warnings.filterwarnings('ignore')
sns.jointplot('^TNX',"^IXIC",df1,kind='reg')
sns.jointplot('^TNX',"^GSPC",df1,kind='reg')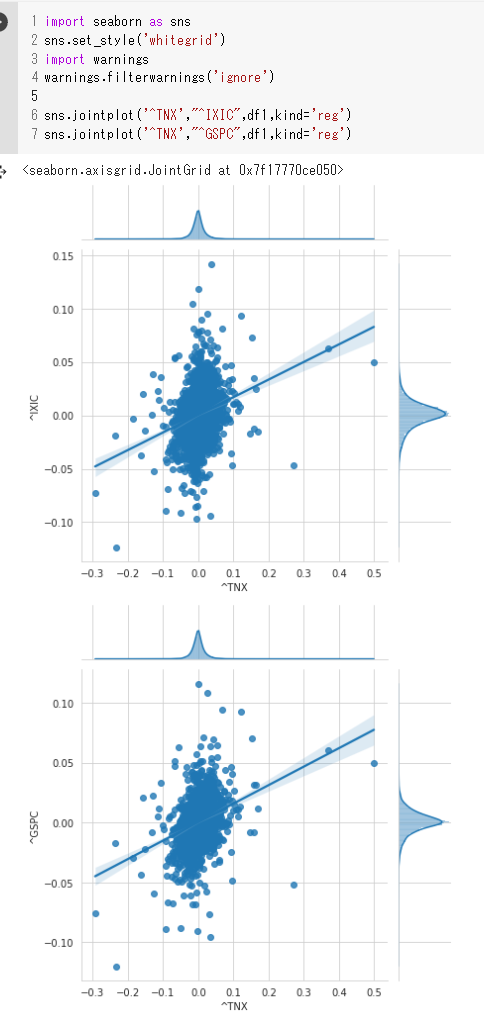
!?この結果は、”利回りが上昇すると株価指数は上昇する”という結果でしょうか。
たしか、利回りが上昇するので、株価指数の下落に気を付けないといけない、、、というのが最近の動向だったはずで、この結果は全く逆なのですが、良かったのでしょうか?
なにかコードにミスをしているかもしれないので、元のデータに戻って確認してみます。
データチェック
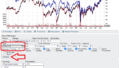
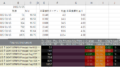
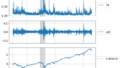
利回りの上昇している区間を二つ指定します。
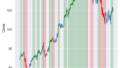
(1998-9-1から2000-1-1)と(2016-7-1から2018-11-1)
その区間の指数の値動きを見てみます。
Zone1_start = datetime.datetime(2016,7,1)
Zone1_end = datetime.datetime(2018,11,1)
Zone2_start = datetime.datetime(1998,9,1)
Zone2_end = datetime.datetime(2000,1,1)
fig = plt.figure()
ax5 = fig.add_subplot(111)
ax6 = ax5.twinx()
ax5.plot(df1.index,(1+df1["^IXIC"]).cumprod(),label="NASDAQ Composite",color="blue")
ax5.plot(df1.index,(1+df1["^GSPC"]).cumprod(),label="SP500",color="orange")
ax6.plot(df1.index,(1+df1["^TNX"]).cumprod(),label="Treasury Yield 10 Years",color="red")
h1, l1 = ax5.get_legend_handles_labels()
h2, l2 = ax6.get_legend_handles_labels()
ax5.legend(h1 + h2, l1 + l2,loc='center left', bbox_to_anchor=(1, 0.5), fontsize=18)
ax5.axvspan(Zone1_start,Zone1_end, color = "gray", alpha=0.3)
ax5.axvspan(Zone2_start,Zone2_end, color = "gray", alpha=0.3)
ax6.grid()
plt.show()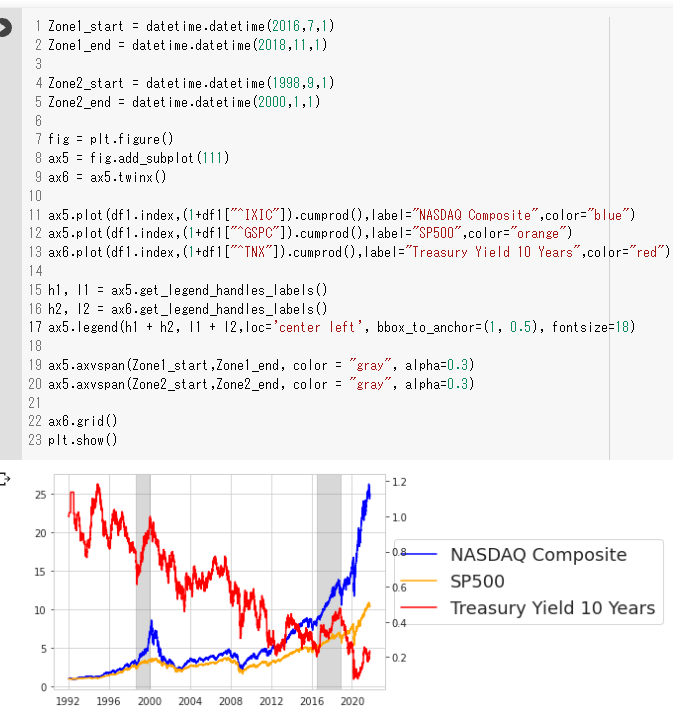
確かに利回りが上昇している間、株価指数とくにハイテクが強く上がっているように見えます。
経済理論的には?
経済理論的なものはどうでしょうか?
大和証券:株はインフレに強いが、デフレに弱い
企業の売上=数量×単価ですから、インフレの時は、単価が上昇するため利益が大きく増加します
という記事もあれば、
SMBC日興証券:金利が上がると株価はどう動く?

継続的に景気が良くなり、金利が上昇する環境下では、(中略)金利上昇と株価上昇が起こります。
反対に、金利上昇が悪い影響を及ぼす場合があります。これは金利が上昇することにより、企業は借入れコストが上昇する為、設備投資の縮小を行います。また、個人消費でも住宅ローン金利が上昇することから、住宅購入を見送ることも考えられ、企業業績低迷への不安が高まり株価は下落する傾向があります。
いったい、どっちでしょうか??
auカブコム証券:逆相関の関係

株式市場と国債市場の関係はシーソーの関係になります。つまり、逆相関の関係ということです。
相関的には順にも逆にもなりそうというあたりさわりのない答えになりそうです。
企業業績に悪影響を与えない程度の金利上昇であれば、株価指数は上がる可能性はあるし、特に会社内に固定資産を持ってないようなハイテク企業については価格の値上げ交渉力があれば、そのまま利益の増加という果実を受け取れるという可能性がありそうです。
先行きの見える水晶玉を持っているわけではないので、あまり断定的なことは言えませんが、
利回り上昇=株価下落
と思考停止的に考える必要はないのではないでしょうか。
ディスクレーマー
投資に関する免責事項情報の提供・作業代行を目的としており、投資勧誘を目的とするものではありません。
---
関連記事を紹介します。
























コメント